Relação de Inclusão

É toda relação entre e exclusivamente dois conjuntos no qual visa comparar e identificar se um conjunto está incluso/contido no outro.

De modo geral, dizemos que um conjunto ‘A’ está incluso/contido em outro conjunto ‘B’ se e somente se todo elemento de A também for elemento de B.

Na primeira ler-se " A está contido em B se e somente se  qualquer que seja x, x pertencer a A  e x pertence a B
na segunda ler-se B contém A. Ambas são iguais.

Representação por diagrama de  A contido em B.

Obs.: quando um conjunto não contém o outro, representamos por:

Em diagramas

Ex.: 

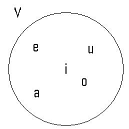
Se o conjunto V = {a; e; i; o; u} e o conjunto A = {a; e} e B= {i; o; b}, podemos afirmar que A está contido em V (ou V contém A), pois todo elemento de A é elemento de V, mas não podemos dizer que V está contido em A porque nem todo elemento de V é elemento de A. Assim como podemos afirmar que B não está contido em V, pois para justificar a inclusão é necessário mesmo que existam elementos em comum que todo elemento de B fosse elemento de V. Neste caso temos:

Propriedades da inclusão:

Pense Bem₁: Seja A = {a; {b}; c}. Atribua valor lógico as afirmações V (verdadeiro) F (falso)

Resposta: V F V F V V F

-Subconjuntos

Seja um conjunto B, e outro conjunto A. Diz-se que B é subconjunto de A, quando este está contido em A, ou seja:

                         

Obs.: os subconjuntos são formados pelos elementos do conjunto.

-Conjunto das partes

É o conjunto formado por todos os possíveis subconjuntos de A

Então se A = {a; b; c}. Todos estes são subconjuntos de A:

B =  {a}           A₁ = {a; b}

A₁ = {b}           A₁ = {a; c}

A₁ = {c}           A₁ = {b; c}

A₁ = {  }           A₁ = {a; b; c}

P(A)={{a}; {a; b}; {b}; {a; c}; {c}; {b; c}; {  }; {a; b; c}}

Contando os subconjuntos temos que n(P(A)) = 8 ma forma mais prática de se encontrar quantos possíveis subconjuntos um conjunto qualquer tem é:

Onde 'n' é o cardinal do conjunto

No caso do conjunto A, temos 3 elementos logo n = 3 então

Pense Bem2 - Se um conjunto A possui 1024 subconjuntos, então o cardinal de A é igual a:

a) 5
b) 6
c) 7
d) 9
e)10

R: 10

Pense Bem3 - Sendo A = { } determine n(P(A))

R: 1

------------------------------------------------------------------------------------
Referências: Vol. 1 Manuel Paiva, Matemática

O que achou do post? Comente. Seu comentário é muito importante para a gente.

A Teoria dos Conjuntos

Define-se conjunto como sendo uma coleção de vários elementos que gozam de uma mesma propriedade.

Como por exemplo, o conjunto das vogais do alfabeto

O conjunto V é o conjunto das vogais formado por "a, e, i o, u".

Formas de representar um conjunto:

-Forma Tabular

Existem três tipos de maneira de se representar um conjunto, a primeira delas seria a representação tabular, que sugere representar um conjunto de forma de uma tabela, escrevendo seus elementos em forma de tabela, entre chaves e separados vírgula ou ponto e vírgula.

Ex.: 

                         

-Representação por Diagrama

Os elementos de um conjunto são representados por pontos e interiores a uma região plana limitada por linha fechada simples:                                           

                      

                       

-Representação Através de uma Propriedade

Se uma propriedade é comum a todos os elementos do conjunto e, se e somente se, estes elementos têm essa propriedade, o conjunto pode ser escrito na forma:

V = { x | x é uma vogal}

Obs.: ler-se V é o conjunto de todos os elementos que é uma vogal (V é igual a x tal que x é uma vogal).

-Tipos de Conjuntos

Conjunto unitário

            É todo conjunto formado apenas por um único elemento.

A = {2}                                                            B = { x | x é a estrela do sistema solar}

Conjunto vazio

A = {.x | x é palavra proparoxítona da, língua portuguesa não acentuada} = { }

Conjunto Vazio em forma de diagrama

                              

-Conjunto Finito

Diz-se que um conjunto é finito quando possível contar a quantidade de elementos há no conjunto

           

Ex.: O conjunto das vogais V = {a; e; i; o; u} possui 5 elementos, portanto é um conjunto finito. Cardinal de um conjunto é o nome que se da ao número de elementos do conjunto, sendo assim, a cardinalidade de V é 5, representado dessa forma.

                               

  n(V) = 5      ou #V = 5

-Conjunto infinito

Diz-se que um conjunto é infinito quando não possível contar a quantidade de elementos há no conjunto

          

  Ex.: O conjunto dos números naturais pares N = {2; 4; 6; 8; ...}

------------------------------------------------------------------------------------
Referências: Vol. 1 Manuel Paiva, Matemática

O que achou do post? comente. Seu comentário é muito importante para a gente.